Solving wordle
Wordle is a simple quiz that is very popular at the moment I’m writing this (but I think we already hit peak-wordle). Users need to guess a target 5-letter word with a trial-and-error approach, similar to the old mastermind, in which you get hints from an oracle as follows: a green tile 🟩 means you nailed the letter and its position; a yellow one 🟨 means the letter is in the word, but in the wrong position; a black one ⬛, the letter is not there at all. If you guess the word in under 6 attempts, you can proudly share your achievement with the world and annoy your social media followers.
What’s the optimal Wordle strategy?
Wordle uses a list of 2315 words that can be a valid solution (and other 10657 additional valid input words). A simple idea is to just pick the input word that will maximally reduce the space of valid solutions, at least on average, across all possible targets.
As an example, consider a word like SMILE. Depending on the target words, the outcome can vary significantly:
- if the target word were CRUEL, the oracle hints would be ⬛⬛⬛🟨🟨 and the solution space would be reduced to 102 solutions;
- if the target word were HINGE, the oracle hints would be ⬛🟨⬛⬛🟩 and the solution space would be reduced to 19 valid solutions;
- if the target word were BUDDY, the oracle hints would be ⬛⬛⬛⬛⬛ and the solution space would be reduced only to 316 valid solutions;
- and so on..
SMILE seems to be a decent, but not spectacular, initial choice: from the full solution space (2315), you can expect to reduce it on average to around 114 valid words.
We can do better than that: applying the same logic, the word that maximally reduces the solution space on average across all possible target words is ROATE. To be honest, I’m not even sure what that means. Picking ROATE as the first guess reduces the number of valid solutions to ~60, on average! On the other hand, choosing the worst ranked word in the vocabulary, IMMIX (?), you wouldn’t cover much ground: you’d still be left, on average, with more than 1300 valid solutions.
Of course, the process doesn’t stop at the choice of the first input. We can iterate until we get to the end, using our 1-step lookahead policy:
- for each valid input word, compute the reduction of the solution space that would be obtained across all possible scenarios (i.e., across all target words that are still valid);
- choose the input word that yields the maximum reduction of solution space size (in expectation);
- get hints from the oracle;
- if you guessed the target word, you’re done!
- otherwise, reduce the solution space according to the hints, and go back to 1.
Note: this can be done in such a naive way because the list of valid words is pretty small, otherwise it would blow up quite quickly.
Does this strategy work at all?
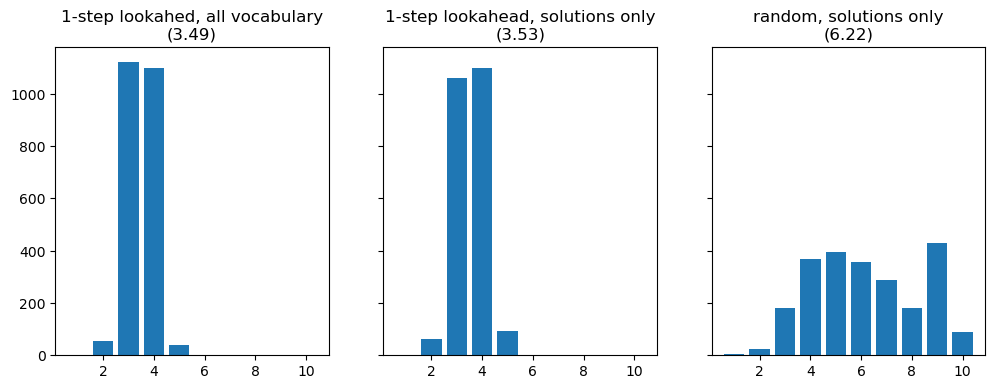
From my simulation, it looks like we would be able to always solve the puzzle in under 6 moves (leftmost plot). The average is slightly below 3.5, which is not bad. You win in ≤3 attempts more than 50% of the time, if you use the entire vocabulary of admissible words (2315 + 10657).
If you only choose inputs from the vocabulary of possible solutions (2315), results are slightly worse (middle plot). Still, in no cases you need 6 attempts, and only very rarely you need 5.
It’s fun to compare the strategy with what happens if you use a totally random choice of words from the valid solutions (rightmost plot): you’d still be able to win (at most 6 attempts) about 57% of the time. (Here I limited to max 10 attempts.)
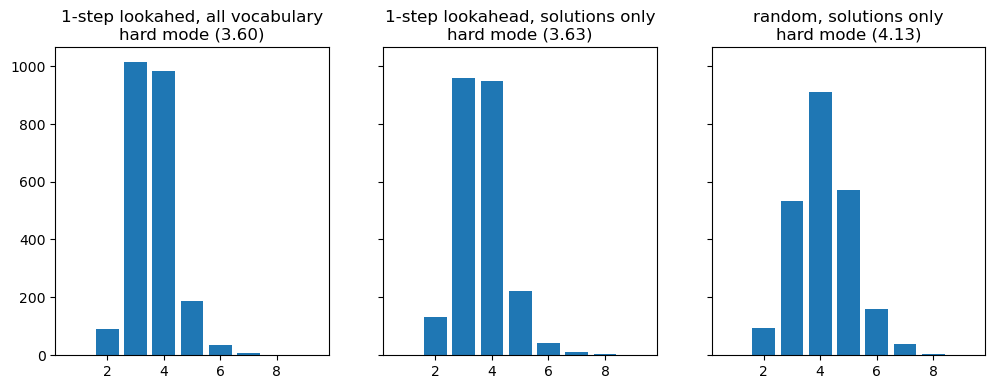
Things do get harder if you play in “hard mode”, that is, all your input words must be consistent with the hints given so far. In this case, you sometimes need up to 8 attempts1. On the contrary, having more constraints greatly helps the “random” strategy: 98% of the time you’d win in 6 or less, and the average number of attempts would be around 4.1.
An example of an unlucky scenario for the lookahead policy in “hard mode” (solutions only) is the word WOUND:
RAISE➝ ⬛⬛⬛⬛⬛ The solution space is restricted to 168 valid solutions.COULD➝ ⬛🟩⬛🟩🟩 The solution space is restricted to 6 valid solutions.BOUND➝ ⬛🟩🟩🟩🟩 The solution space is restricted to 5 valid solutions.FOUND➝ ⬛🟩🟩🟩🟩 The solution space is restricted to 4 valid solutions.HOUND➝ ⬛🟩🟩🟩🟩 The solution space is restricted to 3 valid solutions.MOUND➝ ⬛🟩🟩🟩🟩 The solution space is restricted to 2 valid solutions.POUND➝ ⬛🟩🟩🟩🟩 The solution space is restricted to 1 valid solutions.WOUND➝ 🟩🟩🟩🟩🟩
You could try to use slightly different criteria to rank the input words: I used the average (expected value) over the distribution of possible outcomes, but one could use the worst case (we would pick the input word that would guarantee you the max reduction even in the unluckiest scenario) or even get fancier including some measure of the variance of the outcomes.
How far is this from the optimal policy? Good question. A conceptually trivial extension would be to have a longer horizon, for example, a 2-step lookahed, but it would be quite expensive from a computational point of view.
Small update
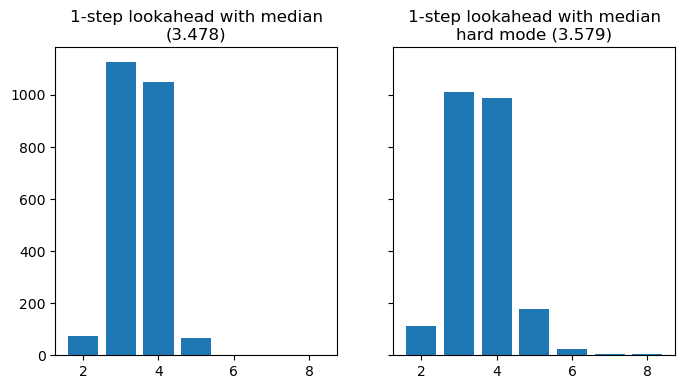
If, instead of the average over the solution space of all possible outcomes, one uses the median, you get even better results. The starting word, in this case, is REIST.
-
You can’t use words that you know are not valid, but would potentially give you a lot of useful information. ↩