Packing Santa's Sleigh
In 2013 Kaggle’s Christmas competition, Santa Claus is asking for help (again). Last year, Santa badly needed routing recommendations. This year, he needs help to pack his sleigh.
Given a list of 1 million presents, the problem requires to pack them in Santa’s sleigh as compactly as possible and following the correct delivery order. The sleigh base is 1000 x 1000, but the tower of presents can grow as tall as necessary. Obviously, Santa would like it to be as short as possible.
The presents have different sizes and are represented by their size in the x, y, and z dimensions. Each present has an ID which determines the order in which it is to be delivered. Ideally, present 1 is to be delivered first, present 2 second, etc. As such, a present with a lower ID must not be packed under a present with higher one. Note that only the z-coordinate of the top side is considered when determining the order.
The presents can be packed in any orientation, provided they are parallel and perpendicular to the x-y-z axes – meaning they can be rotated in any direction only by multiples of 90°.
This boils down to what is known as 3D Bin Packing, with an additional twist given by the z-ordering requirement.
The objective function to minimize is given by the maximum height of the highest present and an ordering term:
\[2 \max_i(z_i) + \sigma(\Gamma)\]where \(z_i\) is the coordinate of the \(i\)-th present and \(\sigma(\Gamma)\) the ordering term: \(\begin{equation}\sigma(\Gamma) = \sum_{i=1}^{N}|i-\Gamma_i|\end{equation}\)
where \(\Gamma\) is the vector of the presents in the order in which they appear from the top, with \(\Gamma_i\) as the id of the present in the \(i\)-th position. Note that the perfect order yields \(\sigma(\Gamma_{\mathrm{ideal}}) = 0\).
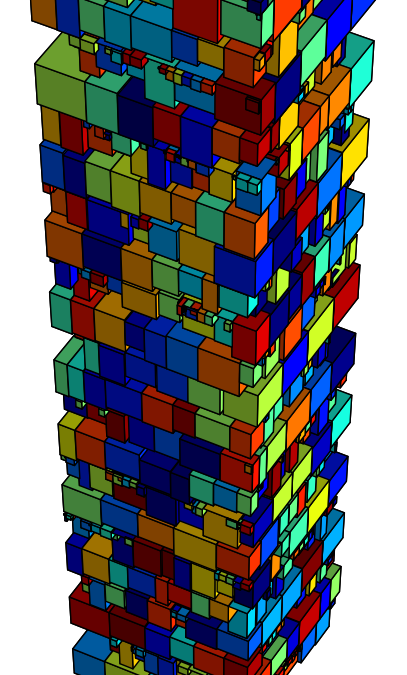
Looking at the number and sizes of the presents, it is easy to verify that the ordering term will easily outweigh the height term, if the order is not accurately taken into account during the optimization. While the height of a respectable – but far from spectacular! – packing is certainly going to be smaller than 1.5M (resulting in a 3M height term in the objective function), the order term can easily skyrocket north of 100 millions… with a worst case (exact reverse order) of \(2\cdot\sum_{i=1}^{N/2}{(N - 2i)},\) which is roughly 500 billions. You can still see submissions with this score in the leaderboard.
So, it is probably necessary, at least as a first approximation, to completely preserve the order. This constraint is strong, but it actually helps in making the problem much easier to solve (at least approximately) – as often the case with combinatorial optimization problems. Indeed, in order to get a rather good solution, it is enough to consider the presents following the delivery order, and pack them in layers, containing presents with their top sides aligned.
Assume that all the presents are rotated with their tallest dimension parallel to the z-axis – a heuristic that seems to work rather well in practice1. Since, by costruction, all presents in the same layer have the same top side z-coordinate (i.e., the order constraint is always trivially fulfilled), this approach moves the problem into another ballpark: (unconstrained) 2D rectangle packing for each layer.
A lot of work has been done on this problem. After a brief literature research and some analysis of the problem data, it looks like the size of the layer packing problem might be too big to allow for an exact approach: more than 4000 layers would have to be packed, with each subproblem usually containing between 150 and 2500 presents.
The time to implement the algorithm being short, my choice falls on a simple polytime heuristic, in the spirit of the ones described here.

The algorithm is an online heuristic that keeps a list of the free rectangles, and attempts to fit a present in the free space where it best fits (short side criterion), rotating it on the x-y plane if necessary. A basic implementation of the layer-by-layer approach with this simple heuristic gives a height of around 1.2M (2.4M score).
The 2D packing density improves if the presents are sorted by decreasing size before you start packing – in particular, the best results seem to be obtained sorting the presents by their second shortest side. This can be done: we don’t want to disrupt the delivery order, but the presents can be reordered as long as they are on the same layer. Ideally we would like to know in advance the exact number of presents that can be packed in the layer by the algorithm, so that we can optimize offline over the entire ‘batch’. This is clearly a chicken-and-egg situation: the batch size itself has to be optimizated. So, for each layer:
- Compute the maximum number K of consecutive presents that could fit in the layer by adding their areas until it exceeds the sleigh’s limits.
- Try to pack all K presents with a 2D packing algorithm
- If a packing can’t be found, decrease the batch size K and go back to 2.
This yields a nice improvement (along with an increase in computing time): 1.035M height, and a score of ~2.07M.
The next step is to improve the 2D packing algorithm. Some simple randomization can be added by considering the order of the presents fed to the heuristic: try to randomize the order in which the heuristic packs the presents, i.e., with a simulated annealing or a genetic algorithm. This leads to obviously longer computational times, and scores that easily reach ~2.02M, although with diminishing returns as the score improves.
Some further tricks are crucial in improving the density of the tower of presents. For instance, we can bubble down the presents in a layer, one by one, provided that the z-order is preserved.
My simple python implementation can be found here. It’s definitely not the most efficient2, and I managed to implement less that what I would have liked to, as the end of the competition approached fast. With a couple of additional tricks – and/or a more efficient implementation – I’m pretty sure this approach can get a score under 2M.
Note that a pure layer-by-layer algorithm, with longest size on the z-axis and no squashing down of the layers, has a lower bound of 1992966 (assuming ‘perfect’ 2D packings3). This score would have guaranteed a top 20 finish, but still wouldn’t have been enough for the first positions.
The scores at the top of the leaderboard suggest that something definitely smarter was going on up there. Indeed, even by keeping a layer approach, much more can be done to minimize the wasted space between layers. For example, a layer packing should be optimized not only with respect to the density of the 2D rectangle fit, but also with respect to the wasted z-space: the tallest presents might be rotated, thus decreasing the height of a layer. In addition, even if the layer is full, it is possible to squeeze a couple of extra presents into the free vertical space. This would be effective especially in combination of a 2D packing with low fragmentation of the wasted z-space.
Thanks to Kaggle and Mathworks for the competition, and congratulations to the teams in the first positions. Looking forward to the next one, it was fun.