For most people nowadays the first programming language is python or javascript. Once upon a time that was not the case, and probably BASIC was the one where most millennials got their feet wet.

That actually never happened for me – I barely knew what “programming” meant before my first university courses, which technically makes Assembly and C my first programming languages. Last week I was skimming through an undergrad level Calculus book (old, but still used by students in Italy), and there I found a juicy chapter on plotting mathematical functions (with 1 or 2 variables) with.. BASIC.

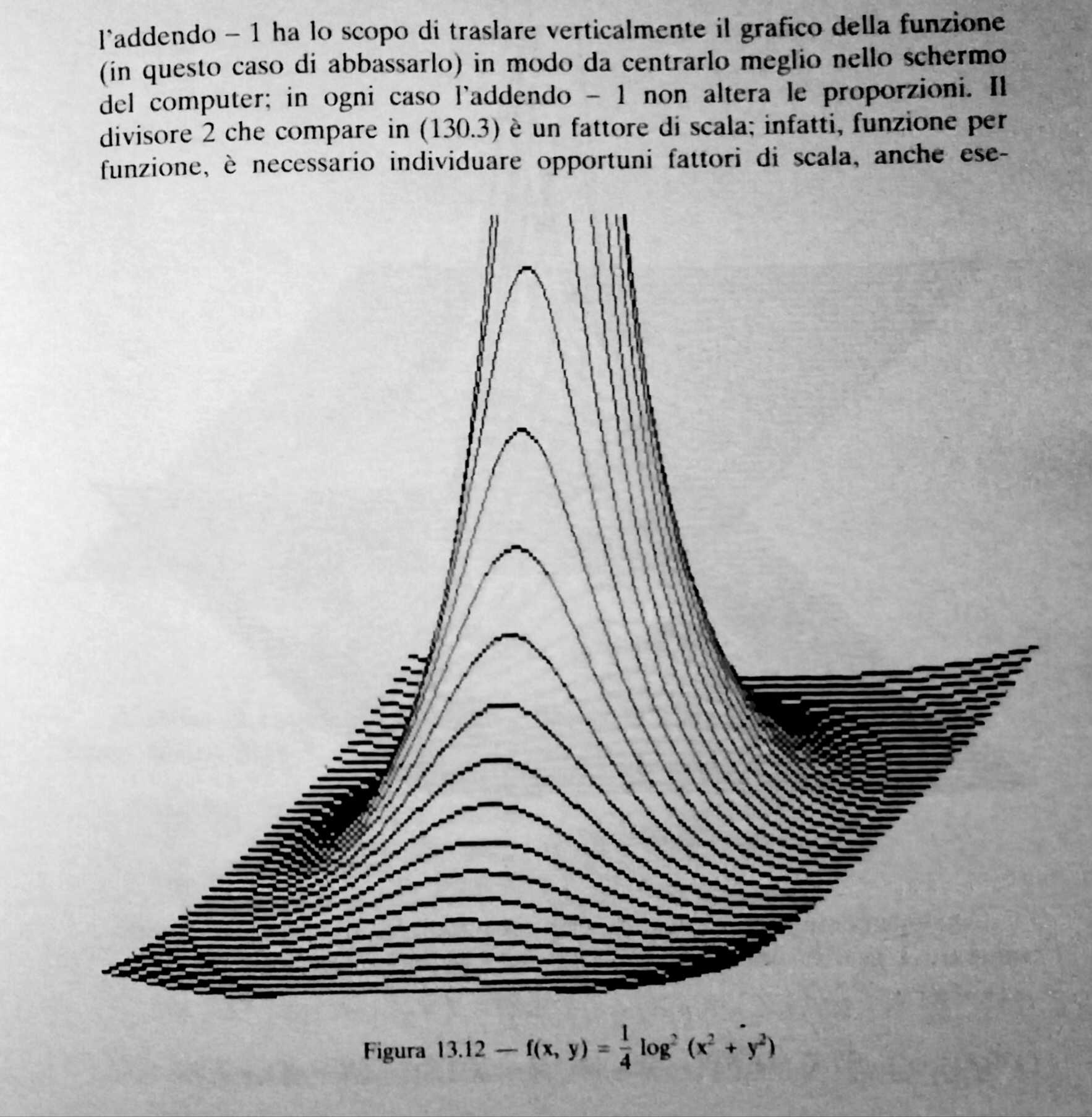
book singularity

I was rather intrigued by the nice looking plots, and how the code actually looked pretty terse! I had to try and replicate those results.

BASIC is more a family of languages than a single one. I picked one that I could easily install on ubuntu (sudo apt install yabasic) and was good to go. This turned out to be a slightly more modern dialect than the one in the book, but the gist is the same.

2d plots

First thing: plotting single-variable functions.

W = 600
H = 600
OPEN WINDOW W,H

X0 = W/2
Y0 = H/2
LINE 0,Y0,W,Y0 //X-AXIS
LINE X0,0,X0,H //Y-AXIS

SUB FUN(X)
    RETURN 200*SIN((X/50))
END SUB

FOR X = 0 TO W
    Y = -FUN(X - X0) + Y0 //invert y coordinate and center in Y0
    LINE X,Y 
NEXT X

In the first block I’m opening a new window with size (W,H). Then I’m plotting the x and y axis in the middle of the window. FUN is the function I want to plot. Finally, a for loop where I need to convert the y value in the actual “window” coordinate (in the output window, the point (0,0) is the upper left corner). The LINE X,Y instruction does the heavy lifting here: if no LINE was previously called, the current point is set to X,Y; otherwise, it draws a line from the previous point to X,Y. Pretty nifty and concise.

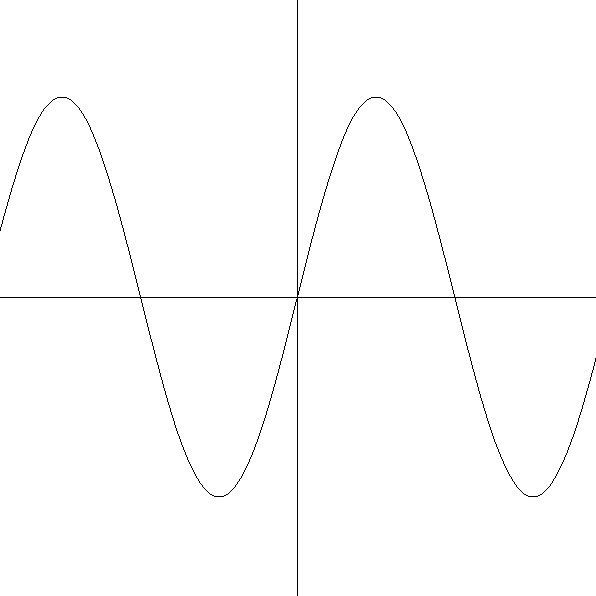
This is the glorious result:

2d sine function

Note that, in the function definition, one needs to make sure the plot can actually be visualized in the window in a decent way – meaning, we need to scale and/or translate it so the window contains something meaningful.

Another easy trick shown in the book is how we can plot a filled curve, where for each X we draw a line between (X,Y) and the x-axis:

FOR X = 0 TO W
    Y = -FUN(X - X0) + Y0 //invert y coordinate and center in Y0
    LINE X,Y0,X,Y
NEXT X

With $y = sin(1/x)$ (and some appropriate scaling) this is what you get: 2d filled function

3d plots

Plotting 2-variables functions in a 3d space is a bit trickier. Given $Z=F(X,Y)$, one needs to transform the $(X,Y,Z)$ point into $(U,V)$-coordinates, that is, the coordinates relative to the window. Let’s assume that $X$ is the axis which is normal to the screen, while $Z$ is the vertical axis and $Y$ the lateral axis. The idea is to draw lines (“slices” of the surface) connecting consecutive points with constant $X$. To give depth and obtain a 3d-ish view, each line is shifted up and right by a small amount of pixels (SHIFT).

W = 1400
H = 1000
OPEN WINDOW W,H
U0 = W/2
V0 = H/2

SUB FUN(X,Y)
    //Define function here    
END SUB

SHIFT = 4
X = 0
NUM_LINES = 80
RADIUS = 600
FOR I=-NUM_LINES/2 TO NUM_LINES //number of lines to plot
    X = I*(W/NUM_LINES)
    NEW CURVE
    FOR Y=-W TO W
        Z = FUN(X,Y)
        U = Y + U0 + I*SHIFT 
        V = -Z + V0 - I*SHIFT
        LINE U,V
    NEXT Y
NEXT I

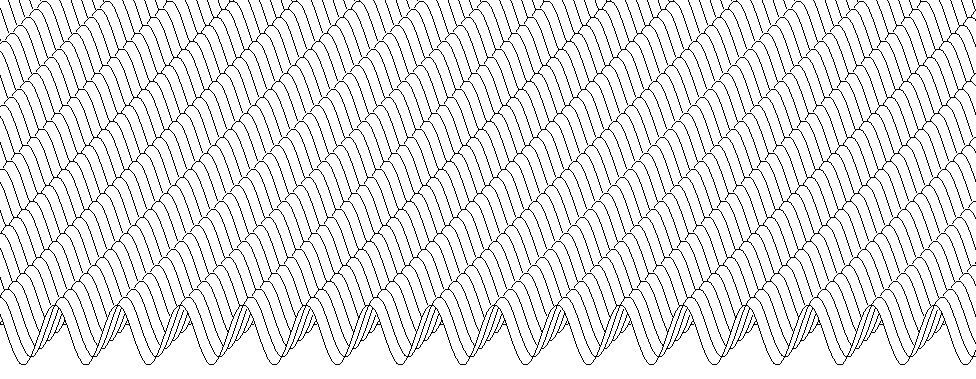
With the NEW CURVE instruction, we stop keeping track of the latest point and a new LINE is started. This code returns a 3d plot, but the result is a bit of a mess even for a simple function like $z = sin(y)$:

3d sin with overlaps

To avoid this issue, one needs to avoid printing lines that are covered by surfaces that are in front of them. We can do that storing the max and min $V$-value for each $U$, so that one can check if a point should be visible.

DIM MAX_V(W), MIN_V(W)
FOR I=0 to W
    MAX_V(I) = -10000000
    MIN_V(I) = 10000000
NEXT I

SHIFT = 4
X = 0
NUM_LINES = 80
RADIUS = 600
FOR I=-NUM_LINES/2 TO NUM_LINES //number of lines to plot
    X = I*(W/NUM_LINES)
    NEW CURVE
    FOR Y=-W TO W
        Z = FUN(X,Y)
        U = Y + U0 + I*SHIFT 
        V = -Z + V0 - I*SHIFT
        IF U >= 0 AND U < W AND V < MAX_V(U) AND V > MIN_V(U) THEN
            NEW CURVE
            CONTINUE
        ENDIF
        IF U >= 0 AND U < W AND V > MAX_V(U)
            MAX_V(U) = V
        IF U >= 0 AND U < W AND V < MIN_V(U)
            MIN_V(U) = V
        LINE U,V
    NEXT Y
NEXT I

This is the correct result for $z = sin(y)$:

3d sin

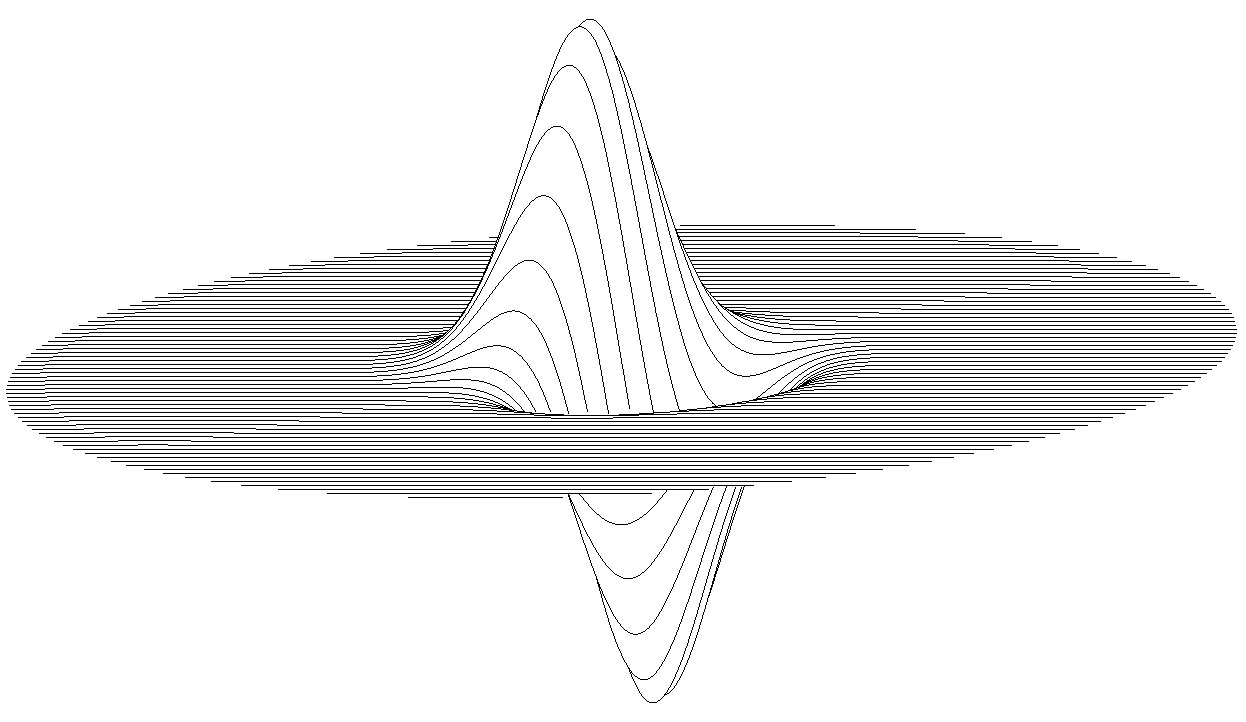
And here’s another example with $z = sin(xy)$:

3d sinxy

We can also add some other eye-candy, like limiting the (X,Y) domain to a circle. Here $sin(x^2 + y^2)$ and $(x-y)e^{-(x^2 + y^2)}$:

3d ripples 3d double peaks